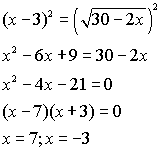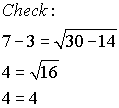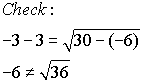Solving Radical Equations

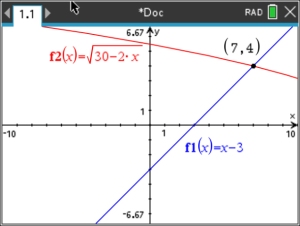
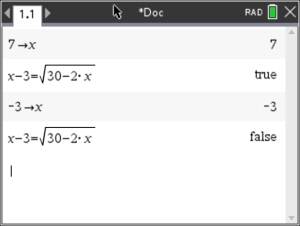
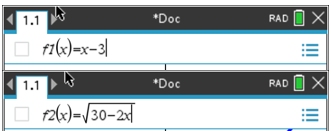
As you know, radical equations involving square roots are typically solved by isolating a radical and squaring both sides of the resulting equation.  This process of squaring may lead to an answer that is actually NOT one of the roots of the original equation.  This "extra" answer is called an extraneous root.  The graphing calculator is a wonderful back-up checking tool to determine if a root is extraneous.  Note the example below:   Example:  Solve the following equation algebraically and check. Algebraic Solution:   Graphical check: Enter the left side of the equation into f1(x). Enter the right side of the equation into f2(x).         Use the INTERSECT option , #6 Analyze Graphs, #4 Intersection x = 7 x = -3 extraneous root The calculator clearly shows that there is only one intersection point, (one solution) at x = 7, thus indicating that x = -3 is an extraneous root.

Hint:  When working with radical equations, it may be difficult to "see" the intersection point if the viewing window is a small representation of the graph.  You may want to enlarge the viewing window by adjusting the WINDOW settings ( , #4 Window, #1 Window Settings).
You can always quickly return to the default viewing window by using #5 ZOOM (Standard).

Remember: In the example above, you can see that there is only one answer to the equation since there is only one point of intersection.  Should there be NO points of intersection, the answer will be the empty set.

Finding Your Way Around TABLE of CONTENTS